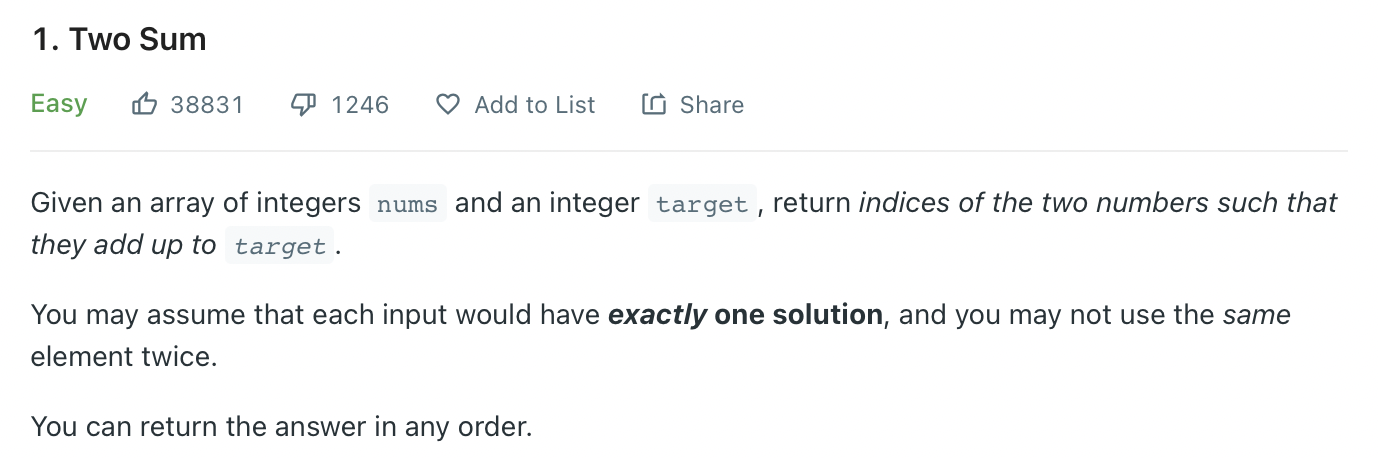

해석)
nums라는 정수 배열과 정수 target이 주어졌을 때, 더했을 때 target이 되는 두 개의 숫자 indices(매핑 정보를 저장하는 데이터 공간..? or 인덱스 복수형) 를 리턴하세요.
각 입력값은 정확히 하나의 솔루션을 가진다고 가정하며, 같은 element(요소, 배열 내 구성을 일컫는 말인가봄) 를 두 번 사용하지 마세요.
순서는 아무렇게나 해서 정답을 리턴할 수 있어요.
시간 복잡도)
O(n^2)
배열 nums를 이중 for문을 돌려서 하나하나 정답을 알아봐야겠다고 생각했다.
이중 for문이기 때문에 nums.length를 고려하는 부분이 중요했는데, 10000 * 10000 => 1억..으로 1초..? 정도로 보면 될 것 같다.
Follow-up 질문이 O(n^2) 시간복잡도보다 적게 걸리는 알고리즘을 생각할 수 있냐는 것이었는데 문제 풀 당시 생각나는 알고리즘은 딱히 없었다.
떠오르는 것은 군데군데 조건을 추가해서 완전한 O(n^2)보다 덜 시간이 걸리게 한다는 생각 뿐..
(예를 들어.. target이 nums[index] + nums[index + a]를 하지도 않았는데 nums[index]보다 클 경우 해당 경우를 pass한다던지..
답이 나왔을 경우 곧바로 리턴..(이건 너무 허접인듯..))
target이 가장 큰 숫자가 1억이었기 때문에 int로 선언해도 문제없었고
구해야하는 nums의 각 요소도 1억 언저리이면서 더했을 때 target이 되는지 확인해야하는데 target이 이미 int인 것이 확실했기 때문에
형식때문에 고민할 일은 없었다
Discuss를 보면서 알게된 알고리즘)
O(n)
hash map에 nums 배열값을 저장하는데, HashMap<nums value, nums index> 이런 식으로 저장했다.
단일 for문이 돌면서 target - nums[index]를 해서 map에 이런 값이 있으면 map의 value값인 nums의 index값을 가지고 나왔다.
HashMap의 get 메소드를 사용해서 target - nums[index] 값의 key가 존재하면 값을 리턴하고
없으면 null을 리턴한다는 것을 바탕으로 null이 아닐 경우 정답일 수도 있겠다..! 에서 착안해서 문제를 풀었다.
제출한 정답)
try 1)

class Solution {
// maximum nums.length 10000
// double for 10000 * 10000 => 100000000 (간당간당..)
public int[] twoSum(int[] nums, int target) {
int nums_size = nums.length;
int[] answer = new int[2];
boolean find_answer = false;
for(int i = 0; i < nums_size; i++) {
for(int j = i + 1; j < nums_size; j++) {
if (nums[i] + nums[j] == target) {
answer[0] = i;
answer[1] = j;
find_answer = true;
break;
}
}
if (find_answer) {
break;
}
}
return answer;
}
}try 2)

import java.util.Map;
import java.util.HashMap;
class Solution {
// O(n)
public int[] twoSum(int[] nums, int target) {
int nums_size = nums.length;
int[] answer = new int[2];
Map<Integer, Integer> nums_map = new HashMap<>();
for(int i = 0; i < nums_size; i++) {
nums_map.put(nums[i], i);
}
for(int i = 0; i < nums_size; i++) {
if (nums_map.get(target - nums[i]) != null && nums_map.get(target - nums[i]) != i) {
answer[0] = i;
answer[1] = nums_map.get(target - nums[i]);
break;
}
}
return answer;
}
}'알고리즘' 카테고리의 다른 글
| [leetcode] Toeplitz Matrix (0) | 2022.10.31 |
|---|---|
| [leetcode] Roman to Int (1) | 2022.10.14 |
| [프로그래머스] 이진 변환 반복하기 (0) | 2022.09.11 |
| [프로그래머스] JadenCase 문자열 만들기 (0) | 2022.09.11 |
| [프로그래머스] 숫자 문자열과 영단어 (0) | 2022.09.08 |